Tutorial:360 degree ender pearl cannon

This tutorial page is a work in progress.

 

Please help expand and improve it. The talk page may contain suggestions.

An ender pearl cannon is a machine that fires an ender pearl to a precise position using explosions for fast player transportation. A 360 degree ender pearl cannon is an ender pearl cannon that can fire within a few blocks of any position in range, in any direction.

A typical ender pearl cannon consists of a few key components:

• An ender pearl aligner that gets the ender pearl to an exact position reliably.
• A source of explosions that can control the amount of explosions produced (usually an array of TNT dupers, but TNT dispensers, ghast fireballs, and wind charges are used as well).
• A basket, which positions the TNT or fireballs so that the explosions occur in reliable positions near the ender pearl.
• A ROM (read-only memory) that stores the explosion counts for many destinations, so that common destinations may be easily used multiple times.
• A user interface to select a destination.

This article only covers the logic that governs the basket, since the other components are used in other devices and fit better in their own tutorial pages. This article assumes the reader already knows how to use redstone proficiently and only needs information about how to design a 360 cannon, not how to physically build one.

The math that allows 360 cannons to work

360 cannons are heavily reliant on linear algebra to work. An understanding of some basic concepts in linear algebra makes understanding 360 cannons much easier. If you are not familiar with linear algebra, it is recommended to skip this section. If you wish to become familiar with linear algebra, there are some fantastic introductory lectures by Gilbert Strang for free on YouTube.

The core game mechanic that makes it all possible is the fact that the velocity given by an explosion to an entity is always identical and is added to the entity's existing velocity. This allows us to treat velocities given by explosions as vectors:

• Two explosion velocities can be added using vector addition. Given two explosion velocities ${\displaystyle v_1=⟨x_1,y_1,z_1⟩}$ and ${\displaystyle v_2=⟨x_2,y_2,z_2⟩}$, their sum is ${\displaystyle v_1+v_2=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩}$.
• An explosion velocity can be scaled by changing the number of explosions in that position. To scale by a negative number, an explosion can be done on the opposite side of the entity to give opposite velocity.

Due to us wanting to hit any position in the 2-dimensional X-Z plane, it will be sufficient to use 2 different explosion positions (and their 2 opposites). Hitting any position in 3D space would require 3 different explosion positions (and their 3 opposites). This is a consequence of the behavior of bases that we will not get into in this article.

Now, assume that we have a basket with A explosions in one position and B explosions in another position. The velocity given to the ender pearl can be written as $${\displaystyle v=A\cdot v_A+B\cdot v_B}$$ where ${\displaystyle v_A}$ is the velocity given by each explosion in the first position and ${\displaystyle v_B}$ is the velocity given by each explosion in the second position. This formula can be expanded to $${\displaystyle \left[\begin{array}{c}x\\ y\\ z\end{array}\right]=A\cdot \left[\begin{array}{c}{x}_A\\ y_A\\ z_A\end{array}\right]+B\cdot \left[\begin{array}{c}{x}_B\\ y_B\\ z_B\end{array}\right]}$$ and finally written as a matrix multiplication $${\displaystyle \left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{cc}{x}_A& x_B\\ y_A& y_B\\ z_A& z_B\end{array}\right]\cdot \left[\begin{array}{c}A\\ B\end{array}\right]}$$ This 3x2 matrix represents the transformation from explosion counts to ender pearl velocity. In general, we wish to do the opposite: given a target velocity, find the explosion counts that will produce it. This requires finding the inverse of the above matrix, which is not possible to do in general because it isn't square. However, it is possible to create an invertible square matrix by using the linear least-squares method: $${\displaystyle \begin{array}{r}{M}^T\cdot M\cdot \left[\begin{array}{c}A\\ B\end{array}\right]=M^T\cdot v\\ \left[\begin{array}{c}A\\ B\end{array}\right]={(M^T\cdot M)}^{-1}{M}^T\cdot v\end{array}}$$ Now compute ${\displaystyle M^T\cdot M}$: $${\displaystyle \left[\begin{array}{c}{v}_A\\ v_B\end{array}\right]\cdot \left[\begin{array}{cc}{v}_A& v_B\end{array}\right]=\left[\begin{array}{cc}\Vert v_A{\Vert }^2& v_A\cdot v_B\\ v_A\cdot v_B& \Vert v_B{\Vert }^2\end{array}\right]}$$ Now compute ${\displaystyle {(M^T\cdot M)}^{-1}}$: $${\displaystyle {(M^T\cdot M)}^{-1}=\frac{1}{\Vert v_A{\Vert }^2\cdot \Vert v_B{\Vert }^2-(v_A\cdot v_B{)}^2}\left[\begin{array}{cc}\Vert v_A{\Vert }^2& -v_A\cdot v_B\\ -v_A\cdot v_B& \Vert v_B{\Vert }^2\end{array}\right]}$$ And finally multiply by ${\displaystyle M^T}$: $${\displaystyle {(M^T\cdot M)}^{-1}\cdot M^T=\frac{1}{\Vert v_A{\Vert }^2\cdot \Vert v_B{\Vert }^2-(v_A\cdot v_B{)}^2}\left[\begin{array}{c}\Vert v_A{\Vert }^2\cdot v_A-(v_A\cdot v_B)\cdot v_B\\ -(v_A\cdot v_B)\cdot v_A+\Vert v_B{\Vert }^2\cdot v_B\end{array}\right]}$$ This is the matrix that transforms ender pearl velocity into explosion counts. Written out in full, it is: $${\displaystyle \begin{array}{rl}{p}_1& =x_1^2+y_1^2+z_1^2\\ p_2& =x_2^2+y_2^2+z_2^2\\ q& =x_1{x}_2+y_1{y}_2+z_1{z}_2\\ E={(M^T\cdot M)}^{-1}\cdot M^T& =\frac{1}{p_1{p}_2-q^2}\left[\begin{array}{ccc}{p}_1{x}_1-q{x}_2& p_1{y}_1-q{y}_2& p_1{z}_1-q{z}_2\\ p_2{x}_2-q{x}_1& p_2{y}_2-q{y}_2& p_2{z}_2-q{z}_1\end{array}\right]\end{array}}$$

Making a basket

Basic basket (4 corners)

The most basic basket allowing 360 degree range has 4 possible explosion positions, but uses only 2 for any given shot. In the case of TNT it is easiest to align it into the corners of blocks.

Ideally the TNT should go as close to the ender pearl as possible. With this basket the pearl goes in the middle, and because of the ender pearl's collision checks with TNT, the closest the TNT can go is 0.79 blocks away from the center. Therefore the biggest block hitbox that can be used on the corners is 11 pixels (most notably flower pots, conduits, and walls with no middle column).

Lava is most commonly used to stop the explosions from destroying blocks. Water also works, but unlike lava it cannot be used in the Nether and changes the ender pearl's movement. It is common to hold up the TNT using fences under the lava because raycasts cannot hit the top part of the fences and obstruct the explosion (see Explosion#Edge cases for more about the exposure raycasts).

Choosing a direction

Each pair of TNT positions can reach only one out of the 4 quadrants of the world. With the pictured slime block layout, there is always one slime block that stays retracted and one that extends. To calculate TNT counts you need to first decide which quadrant the destination is in, and then use those two explosion positions for the rest.

"Differential" basket

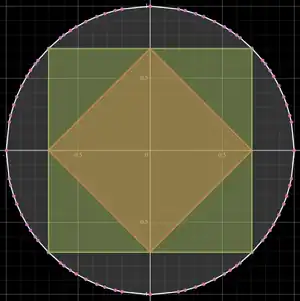
The simple 4-corner basket has a major inefficiency: The two corners of TNT come from different sources. This means that, for example, shooting along a perfect diagonal uses at most half of the available TNT in the whole cannon. It would be more efficient if the total amount of TNT could be split in any ratio between the two corners. This is the concept of the "differential" basket. The name comes from the differential used in the drive of wheeled robots, specifically the "swerve" drive used commonly in FTC robotics.

In order to get the TNT in any ratio, the TNT enters the basket and is then separated using entity stack separation. This can be done using a trapdoor or fence gate activated by a pressure plate, but it's usually easier to use other TNT. Here is the required update order when using TNT:

1. All the main TNT is aligned into the exact same position.
2. Upwards or downwards acceleration TNT explodes. This is necessary so that one of the two "corners" doesn't affect the other. The main TNT needs to be given at least 8 blocks/tick of velocity (or 8.04 when accelerating upwards to counteract gravity) so that it moves out of explosion range in a single tick.
3. Sideways acceleration TNT explodes. The purpose of this is to get the first "batch" of TNT the required velocity to hit a corner. After this step the main TNT should all have above 8 blocks/tick of velocity in Y and diagonal velocity in X and Z.
4. First "batch" of main TNT ticks. It moves vertically from its starting point, then diagonally to its final position in the first "corner", then explodes there.
5. Stack separation TNT explodes. Only the second "batch" of main TNT, which hasn't ticked yet, is affected. It is given the velocity required to cancel its existing horizontal velocity and end with enough to reach the second "corner".
6. Second "batch" of main TNT ticks. It moves vertically from its starting point, then diagonally to its final position in the second "corner", then explodes there.

Encoding schemes

This section is a work in progress.

 

Please help expand and improve it. The talk page may contain suggestions.

There are many different possible ways to encode the TNT sources to produce TNT in the correct order. For ease of wiring, it is generally good to minimize the amount of TNT that needs to switch batches.

Variable bit strategy

One way to encode a differential basket is to have a "variable bit". The strategy is based off of the assumption that one corner of the basket will always have an explosion count larger or equal to the other. By default, we assume that the early corner is always the smallest. This allows us to have 2 sides to the cannon: the "simple side" that has all its TNT on the late order, and the "complex side" that has some TNT in each order.

Notice that when the amount of explosions on each corner is less than half of the total TNT count, the simple side will be entirely late TNT and the complex side will be entirely early TNT. When more TNT is needed on the late corner, we can encode with the following strategy:

• Fill the complex side with all required early TNT, which is guaranteed to be less than half of the total TNT.
• Fill the rest of the complex side completely with late TNT. This amount is also guaranteed to be less than half of the total TNT.
• Fill the remaining late TNT needed in the simple side.

Now if we need more TNT on the early corner, we can swap the entire simple side to produce late TNT and use the same strategy:

• Fill the complex side with (half the total TNT) - (required late TNT) early TNT, which is guaranteed to be less than half of the total TNT.
• Fill the rest of the complex side completely with late TNT. This amount is also guaranteed to be less than half of the total TNT.
• Fill the remaining early TNT needed in the simple side.

This scheme requires 2 additional bits of information compared to a simple basket:

• A "variable bit" which enables all disabled TNT on the complex side but with a later order.
• A "side swap bit" that toggles the order of the simple side.

One important observation is that the "side swap bit" will only be on if the "variable bit" is also on. This allows both to be represented as a single ternary number: 0 if both corners have less than half the total TNT, 1 if more TNT is needed late, and 2 if more TNT is needed early. In total this means that encoding a cannon with 2^N TNT requires 2N + 1.5 bits of information.

Here is a table comparing the functionality of each bit in the encoding between a simple basket and a differential basket:

Circle basket

There is still another inefficiency in the differential basket. Acceleration is most efficient along the 4 fixed explosion positions, but shooting exactly in between two of the explosion velocity directions is inefficient. It would be better if we could position every explosion in one place and be able to change freely where that place is, which would give a circular range instead of a square range.

However, putting every TNT in the same position is also inefficient. In order to have the same precision as a differential basket, there would have to be an entire cannon of TNT just to position the explosions accurately enough. This would end up doubling the amount of total TNT, where half is used to position the explosion and the other half explodes in that position. In the circle basket we find a better compromise.

The idea is to use the differential basket technology with 2 explosion positions, but choose the 2 positions freely from a grid of possible positions. In order for the explosion efficiency to be optimal the grid needs to be as small as possible. To achieve this we can use the same TNT-based TNT separation technology from the differential basket, but with multiple side acceleration TNT. Each one needs to give the main TNT the minimum possible motion to keep the grid small.

The size of the grid does not need to be very large to approximate a circle very closely. In the differential basket, 4 possible points gave a square. Here, a 3x3 grid gives an octagon, a 5x5 grid gives a 16-gon, a 7x7 grid gives a 32-gon, a 9x9 grid gives a 48-gon, and so on (these numbers are 8 times the totient sum function). See the desmos graph for a visualization of the true shape of the range.

Once the basket is set up, the encoding is done the same way as the differential basket. However, note that for most target destinations there are multiple pairs of explosion points that can reach it. You may decide if you want to consider all possible pairs; the most efficient pair is always the two points whose velocities point closest to the target, and considering the other pairs gives you a chance to get higher accuracy at the cost of TNT effiiciency.

Calculating how many explosions to use

1. Decide on the explosion points

The first step is to decide which explosion points will be used for the shot. If using a basic 4-corner basket, this means choosing which quadrant the destination is in. For more complicated baskets you may need to repeat this whole calculation (steps 1-5) for multiple pairs of points to pick the best one.

2. Note the explosion velocities

The second step is to write down the velocity given by each explosion point to the pearl. The easiest way to get the velocities is to use the carpet mod to print them using /log explosions full. This will let you click on the velocities in your chat and copy them directly, skipping this whole step. If you don't have the mod, the next best thing is to use the explosion entity influence calculator:

3. Compute the velocity to explosion count matrix

The easiest way to convert a target velocity into explosion counts is to use a matrix multiplication. We will call the matrix that transforms ender pearl velocity into explosion counts ${\displaystyle E}$. It is always the same for the same 2 explosion points. For two explosion velocities ${\displaystyle v_1=⟨x_1,y_1,z_1⟩}$ and ${\displaystyle v_2=⟨x_2,y_2,z_2⟩}$, the ${\displaystyle E}$ matrix is given by: $${\displaystyle \begin{array}{rl}{p}_1& =x_1^2+y_1^2+z_1^2\\ p_2& =x_2^2+y_2^2+z_2^2\\ q& =x_1{x}_2+y_1{y}_2+z_1{z}_2\\ E={(M^T\cdot M)}^{-1}\cdot M^T& =\frac{1}{p_1{p}_2-q^2}\left[\begin{array}{ccc}{p}_1{x}_1-q{x}_2& p_1{y}_1-q{y}_2& p_1{z}_1-q{z}_2\\ p_2{x}_2-q{x}_1& p_2{y}_2-q{y}_2& p_2{z}_2-q{z}_1\end{array}\right]\end{array}}$$ For example: here is the ${\displaystyle E}$ matrix for a 4-corner basket with a perfectly aligned pearl, being used to calculate the TNT counts to give the pearl ${\displaystyle ⟨20,0,10⟩}$ velocity: $${\displaystyle \begin{array}{rl}& E=\left[\begin{array}{ccc}0.829747854350168& 0& 0.829747854350168\\ 0.829747854350168& 0& -0.829747854350168\end{array}\right]\\ & \left[\begin{array}{ccc}0.829747854350168& 0& 0.829747854350168\\ 0.829747854350168& 0& -0.829747854350168\end{array}\right]\cdot \left[\begin{array}{c}20\\ 0\\ 10\end{array}\right]=\left[\begin{array}{c}24.892435630505037\\ 8.29747854350168\end{array}\right]\end{array}}$$ From that calculation, you find that the TNT counts that get you closest to the target are 25 and 8 respectively.

See the all in one calculator to compute ${\displaystyle E}$ automatically.

4. Calculate the required ender pearl velocity

{
    "title": "Ender Pearl (entity)",
    "rows": [
        {
            "field": "Acceleration, Drag, Position",
            "label": "Ticking order"
        },
        {
            "field": "0.03 ([https://en.wikipedia.org/wiki/Double-precision_floating-point_format double])",
            "label": "Gravity"
        },
        {
            "field": "0.99 ([https://en.wikipedia.org/wiki/Single-precision_floating-point_format float])",
            "label": "Drag"
        },
        {
            "field": "2.97 b/t (59.4 m/s)",
            "label": "Terminal velocity"
        },
        {
            "field": "99 blocks per b/t of initial velocity",
            "label": "Maximum travel"
        }
    ],
    "invimages": [],
    "images": []
}

There are multiple possible trajectories depending on how many ticks the pearl flies for. It is recommended to calculate the explosion counts for all of them and at the end select the one that best fits your needs (the one that gets closest to the destination, the one that arrives fastest, the one that uses the least explosions, etc).

The ender pearl's displacement refers to how far you want it to move from its starting position: ${\displaystyle \text{displacement}=\text{target position}-\text{start position}}$.

The formula for the ender pearl's displacement after ${\displaystyle t}$ ticks starting with velocity ${\displaystyle v_0}$ is $${\displaystyle \text{displacement}=\frac{d(1-d^t)}{1-d}(v_0-\frac{d}{1-d}a)+\frac{dt}{1-d}a}$$ with d = 0.9900000095367432 and a = [0.0, -0.03, 0.0].

Therefore, you can calculate the required velocity by inverting the above formula: $${\displaystyle v_0=\frac{1-d}{d(1-d^t)}(\text{displacement}-\frac{dt}{1-d}a)+\frac{d}{1-d}a}$$ You should now have a value for the initial velocity ${\displaystyle v_0}$ for each possible tick length ${\displaystyle t}$. See the all in one calculator to have this done automatically.

5. Put it all together

Now that you have the initial velocity required to hit the target for every possible travel time, you can feed them into the matrix from step 3 and get explosion counts for each one. You will need to round the outputs of the matrix multiplication so that they represent a discrete amount of explosions.

All in one calculator

Due to the limit for maximum calculations on a wiki page, no more than 30 ticks of data can be shown here.

Examples

Here are a few curated examples of 360 ender pearl cannons for various game versions and basket types. There is also a playlist on YouTube with all known 360 cannon videos on the platform.

Navigation

v t e Tutorials
Introductory Basics Menu screen Java Edition Bedrock Edition Game terms Playing with a controller Newcomer survival Beginner's guide First ten minutes Second day Third day Best biomes to use Hunger management Things to do Things not to do Simple tips and tricks Shelters Best biomes for homes Best building materials Building and construction Navigation Shelters Types
General General Achievement guide Legacy Console Edition Advancement guide Minecraft Nether The End Adventure Husbandry Adventuring Best enchantments guide Breaking a fall Breaking bedrock Chunk loader Combat Complete main adventure Creating a village Dual wielding Desert survival End survival Exploring caverns Gathering resources on peaceful difficulty Getting food quickly Getting max gear Headless pistons Hitboxes Horses Indestructible end crystals Managing slimes in superflat mode Mapping Measuring distance Minecraft in education Mining Ancient debris Diamonds Fossils Nether hub Nether portals Nether survival Organization Pillar jumping Phantom-proofing Spawn-proofing Summoning jockeys Things to do when bored The Void Thunderstorm survival Time-saving tips Transportation methods Units of measure Village mechanics Trading X-ray glitches Zombie siege defense Enchanting and smelting Enchanting Anvil mechanics Automatic smelting Manual smelting
Challenges General Acquiring a conduit Archaeology Curing a zombie villager Conquering a mountain Defeating a bastion remnant Defeating an End city Defeating a monster room Defeating an ocean monument Defeating a Nether fortress Defeating a pillager outpost Defeating a stronghold Defeating temples Defeating trial chambers Defeating a woodland mansion Defeating a village raid Defeating the Ender dragon Defeating the Wither If it escapes Exploring an ancient city Locating a stronghold Obtaining every music disc Obtaining every block Obtaining every item Non-standard survival Adventure mode survival Custom maps Half hearted hardcore Hardcore mode Surviving in a single area for a long time Infinite desert survival Island survival Manhunt Mob switch Nomadic experience Trapping every mob Skyblock survival Skywars survival Speedrunning Starting in the Nether Starting in the End Superflat survival Java Edition Bedrock Edition Ultra hardcore survival The World Starts With One Getting to the world border Village only survival Challenge maps Beating a challenge map Creating a challenge map
Constructions Constructions Adding beauty to constructions Airlock Architectural terms Building a cruise ship Building a metropolis Building a rollercoaster Building micro shelters Building safe homes Building water features Chunk ban Color palette Creating shapes Defense Elevators Endless circling pool Furniture Glazed terracotta patterns Making nice floors Pixel art Ranches Roof types Curved roofs Roof construction guidelines Roof decorations Secret door Settlement guide Underwater home Walls and buttresses Water gate Water-powered boat transportation Block breaking Blast chamber Igniting TNT underwater Wither cage
Farming Blocks and items Amethyst Armor Azalea Bamboo Basalt Bedrock Beetroot Blaze Rod Bone Meal Cactus Carrot Cat gift Chorus Fruit Clay Cobblestone Cocoa Beans Copper Dirt Dragon's breath Dripstone Egg Enchanted Golden Apple Experience Fern Fish Flower Froglight Ghast Tear Glow Berries Glow Ink Sac Glow Lichen Goat Horn Gold Hanging Roots Honey Ice Iron Kelp Lava Meat Moss Mud Mushroom Music Disc Tutorial:Drowned farming Nether growth Nether vine Nether Wart Obsidian Ominous Bottle Potato Powder Snow Pumpkin, Melon Resin Clump Rooted Dirt Sculk Turtle Scute Seagrass Sea Pickle Snow Soul Soil Sugar Cane Sweet Berries Tree Trident Vine Villager trading hall Wheat Wither Rose Wool Duplication Mobs Mob farming Mob grinding Monster spawner traps Allay Animals Axolotl Bee Blaze Breeze Cat Cave Spider Chicken Creaking Creeper Drowned Ender Dragon Enderman Fox Frog Ghast Glow squid Goat Guardian Hoglin Iron golem Magma cube Phantom Piglin bartering Pillager Raid Shulker Skeleton horse Silverfish Slime Squid Turtle Villager Wandering trader Warden Witch Wither Wither Skeleton Wolf Zombie Zombie villager Zombified piglin
Mechanisms Various devices Redstone Circuits Components Dust Mechanics Tips Automatic respawn anchor recharger Combination locks Command block Crafter Flying machines Hopper TNT Item sorting Item transportation Mechanisms Observer stabilizer Randomizers Redstone music Doorbell Rube Goldberg machine Shulker box storage Detectors Block update detector Comparator update detector Daylight detector Minecarts Train station Minecarts Storage Storage system Traps Snow golems TNT cannons Trapdoor uses Trap design Traps Pistons Piston uses Piston circuits Quasi-Connectivity Zero-ticking Instant repeaters Tripwire Tripwire techniques Advanced redstone Advanced redstone circuits Arithmetic logic Calculator Command stats Hourly clock Morse code Printer Redstone computers Redstone telegraph 360 degree ender pearl cannon
Multiplayer General Griefing prevention Hiding chests Multiplayer Survival Spawn jail Playing on servers PvP Java Edition Bedrock Edition Bases Joining a LAN world with alternate accounts Server setup Setting up a Java Edition server Forge server Hamachi server Setting up a Bedrock Edition server Server maintenance Setting up a LAN world Server startup script FreeBSD OpenBSD Ubuntu Ramdisk enabled server
Technical General Creating Forge mods Moving structures using structure blocks from world to world Improving frame rate Minecraft help FAQ Note Block Studio Programs and editors Running the data generator Update Java See Minecraft's code Downgrading Restoring a hardcore world Obtaining discontinued objects Adding profiles to the new launcher Useful commands Maps Custom maps Map downloads Command NBT tags Falling blocks Updating old terrain using MCEdit Resource packs Creating a resource pack Loading a resource pack Models Sound directory making custom panoramas Data packs Adding a new dimension Adding custom enchantments Adding custom paintings Adding custom trims Creating a data pack Custom structures Installing a data pack Repairing a world corrupted by a data pack Creating Minecraft media Creating videos Livestreaming Hide Server IP Game installation Installing versions Installing Minecraft Preview and beta versions How to get a crash report Installing Forge mods Custom Minecraft directory Playing and saving Minecraft on a thumb drive Recover corrupted saved world data Run Minecraft through Google Drive Save game data to Dropbox (world data only) Saved data Dropbox guide Create a Mac OS X startup daemon Playing Java Edition on ChromeOS
Outdated Farming Potion farming End of light mob farms Door-based iron golem farming Villages Legacy Console village mechanics Pre-1.14 village mechanics Village chaining Glitches Duplication Far Lands Contraptions Minecart booster Repeater reboot system Instant wire Water ladder Water tram Challenges Survival with no enabled data packs Construction Man-made lake Other Custom texture packs How to get a crash report (old) Installing mods Setting up a Spigot server Update LWJGL Update Minecraft Custom world generation Playing and saving Minecraft on a thumb drive with the old launcher