Tochio's Computation on the Soroban/Poly-Division
POLY-DIVISION.
Remember the following tables which are used in conjunction with the Mono-division tables and may be considered as forming part of each respective division table:—
| Reverse division 1, make 9 & (suffix) 1. | 1 reversed gives 1 |
| 2 reversed„ gives„ 2[1] | |
| 3 reversed„ gives„ 3[1] | |
| 4 reversed„ gives„ 4[1] | |
| Reverse division 2, make 9 & (suffix) 2. | 1 reversed gives 2 |
| 2 reversed„ gives„ 4[1] | |
| 3 reversed„ gives„ 6[1] | |
| Reverse division 3, make 9 & (suffix) 3. | 1 reversed gives 3 |
| 2 reversed„ gives„ 6[1] | |
| Reverse division 4, make 9 & (suffix) 4. | 1 reversed gives 4 |
| Reverse division 5, make 9 & (suffix) 5. | 1 reversed gives 5 |
| Reverse division 6, make 9 & (suffix) 6. | 1 reversed gives 6 |
| Reverse division 7, make 9 & (suffix) 7. | 1 reversed gives 7 |
| Reverse division 8, make 9 & (suffix) 8. | 1 reversed gives 8 |
| Reverse division 9, make 9 & (suffix) 9. | 1 reversed gives 9 |
Remark.—Rev div. 1, make 9 & 1, and 1 reversed gives 1, etc., belongs to the 1st division. Rev. div. 2, make 9 & 2, and I reversed gives 2, etc., belongs to the 2nd division. Similarly all the others be-long to the respective divisions.
These tables are used only when the divisor is greater than the dividend in corresponding number of columns of the latter, the left hand part of the tables being applied when dividend column has the same figure as the Indicator. They are not very difficult to remember, since, when we say Reverse division 1, etc, the dividend column is made 9 and the original figure (Indicator) is suffixed, and, when we say 1 reversed gives 1, etc., 1 is taken from already divided column and the Indicator figure is inserted in the next column.
They may be explained thus:—
| Rev. div. 1, make 9 & 1 | 1 ) 10 ( = 9 | 1 part of each quotient, when reversed to next column, corresponds to the respective Indicator | |
| 9 | |||
| ——— | |||
| 1 ——suffix | |||
| Rev. div. 2, make 9 & 2 | 2 ) 20 ( = 9 | ||
| 18 | |||
| ——— | |||
| 2 ——suffix | |||
| Rev. div. 3, make 9 & 3 | 3 ) 30 ( = 9 | ||
| 27 | |||
| ——— | |||
| 3 ——suffix |
Rule 6.—Poly-division.—Divide each column of the dividend individu-ally, commencing from the highest column, by the indicator and subtract the product of the partial quotient and the other columns of the divisor from the following columns of the dividend.
Let us now see how the division is performed.
144 ÷ 12 = 12.
Fig. 22.
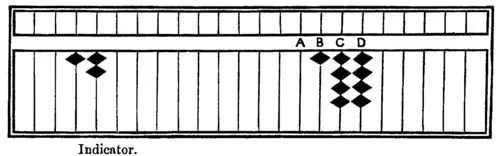
As the Indicator is 1, the 1st division table is employed. 1 is once—clear B and forward 1 to A, and then deduct in C, product 2 of A × the 2nd column of the divisor. Now, you have 2 in C. 2 is twice—forward 2 and 2 * 2 = 4 is deducted in D, completing the division.
No. 3.—The multiplication table, when employed in division, should be read in subtracting sense, viz: 1 × 2 = 2, 2 × 2 = 4 should be rend 1 × 2 MINUS 2, 2 × 2 MINUS 4, and so forth.
192 ÷ 16 = 12.
Fig. 23.

B. 1 is once; 1 × 6 minus 6 (in C)
C. 2 is twice; 2 × 6 minus 12 (in C & D)
Although we had 3 in C, we have forwarded 2 only to B, otherwise we cannot subtract the product of the 2nd column of the divisor. Should you forward 3 saying 3 is thrice, you could take 1 from 3 in B and add 1 to C, saying 1 reversed gives 1.
10,000 ÷ 16 = 625.
Fig. 24.

In this division, the 1st division table applies also, the Indicator being 1. Now, if you forward 1 to A saying 1 is once, there is no means to subtract the product of 1 × 6, and the figure in B being smaller than the divisor, you have to take the reverse table. Reverse division 1, make 9 & 1—B is made 9 and C gets 1. But, you cannot subtract 9 × 6 minus 54 in C & D, therefore you have to reverse 3 from B, saying 3 reversed gives 3. C column is now 4 and B 6. Subtract then in C & D, 6 × 6 minus 36. You now have 4 in D. 2 is twice and C gets 2 and 2 × 6 minus 12 subtracted in D & E, leaving 8 in column E. 5 is 5 times—take 5 from E and forward 5 to D. Next, 5 × 6 minus 30, is deducted in columns EF, subtraction extending to the unit and completing the division.
272 ÷ 16 = 17.
Fig. 25.
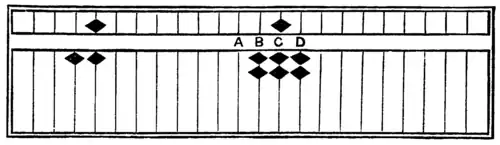
B. 1 is once; 1 × 6 minus 6 (deduct from C).
If you have forwarded 2 to A column and find that you cannot deduct the product 12, you may reverse 1 from A and giving B 1, saying 1 reversed gives 1.
The remaining 1 in B has not been divided yet, therefore, again in B. reverse division 1, make 9 & 1; 2 reversed gives 2; 7 × 6 minus 42.
In reversing from B to C, if you find that you have over-reversed figures, you can again forward back, saying 1 is once or 2 is twice as per table, as the circumstances may require.
These remarks also applies to Fig. 24.
2047 ÷ 23 = 89.
AB
The indicator is 2, therefore use the 2nd division table.
A. Rev. div. 2, muke 9 & 2; 1 reversed gives 2; 8 × 8 minus 24.
B. Rev. div. 2, make 9 & 2; 9 × 3 minus 27.
3204 ÷ 36 = 89.
AB
The Indicator is 3, therefore, the 3rd division table is used.
A. Rev. div. 3, make 9 & 3; 1 reversed gives 3; 8 × 6 minus 48.
B. Rev. div. 3, make 9 & 3; 9 × 6 minus 54.
45756 ÷ 492 = 93.
ABCDE
The Indicator is 4, therefore, the 4th division table is used.
A. Rev, div. 4, make 9 & 4; 9 × 9 minus 81; 9 × 2 minus 18 (in CD).
B. 4th pr. 1, make 2 & 2; 4 is once (C to B); 2 × 9 minus 27; 8 × 2 minus 6 (E).
5046 ÷ 57 = 88.
AB
The Indicator is 5, therefore, the 5th division table is used.
A.—Rev. div. 5, make 9 and 5; 1 reversed gives 5; 8 × 7 minus 56.
B.—5th pt. 4 double 4; 8 × 7 minus 56.
547272 ÷ 792 = 691.
ABC
The Indicator is 7, therefore, the 7th division table is used.
A.—7th pt. 5, make 7 and 1; 1 reversed gives 7; 6 × 9 minus 54; 6 × 2 minus 12.
B.—Rev div. 7, make 9 and 7; 9 × 9 minus 81; 9 × 2 minus 18.
C.—7 is once; 1 × 9 minus 9; 1 × 2 minus 2.
998001 ÷ 999 = 999.
ABCDEF
The Indicator is 9. Use the 9th division table.
A.—Rev. div. 9, make 9 and 9; 9 × 9 minus 81; 9 × 9 minus 81.
B column cannot receive 9, therefore, you may either deduct the first product in mind and the second product also, inserting 9 in column D, or deduct 81 first and add 9 to B; and take 1 from B which corresponds to 10 in C where 80 is deducted and taking 1 from C which corresponds to 10 in D, 1 is deducted in D leaving 9 in that column.
B.—Rev. div. 9, make 9 and 9; 9 × 9 minus 81; 9 × 9 minus 81. Operate in similar way as in A.
C.—9th pt. 8 subjoin 8; 9 is once (not necessary to add 8 to D, which cannot receive same, but take 1 from D and forward 1 to C); 9 × 9 minus 81; 9 × 9 minus 81.
Note.—In the foregoing examples and in mono-division (vide No. 2), you will observe:
That the highest partial quotient always occupies the foremost column of the dividend irrespective of the divisor being one column or more, and that, in mono-division, the Unit of the quotient is located one place to the left of the original unit column; in two-column division, two places; and, in three-column division, three places.
Hence:—
Rule 7.—In division, the unit ascends in the quotient as many columna as in the divisor.
Note.—See remark under Rule No. 4.